Reduction formulae is a method of integration commonly used in solving integrals that are raised to power n. It is common in trigonometric ratios that are raised to power n.
Reduction formula is obtained using implicit integration. implicit integration is the use of substitution to find the integral of y with respect to x. This method only works if the derivative of the substituted function is already in the integral. It is basically use of chain rule(PhysicsForums.com )
Using the implicit integration, obtain the reduction formulae for:
$$I_n = \int cos^nxdx \ hence \ evaluate \ \int cos^5dx$$
solution
$$I_n = \int cos^nxdx =\int cos^{n-1}cosxdx$$
taking the part with the highest power;
we let u = cosn-1 x and dv= cosxdx
$$\frac{du}{dx} = (n-1)(-sinx)cos^{n-2}$$
hence
$${du} = (n-1)(-sinx)cos^{n-2}{dx}$$
$$\int dv = \int cosxdx= sinx$$
hence v =sinx and then substituting in the integral:
$$I_n = sinxcos^{n-1}x +(n-1)\int sin^2x cos^{n-2}xdx$$
From the trigonometric identities:
$$sin^x = 1-cos^2x$$
hence we have :
$$I_n = sinxcos^{n-1}x +(n-1)\int (1-cos^2x) cos^{n-2}xdx$$
expanding the integral:
$$I_n = sinxcos^{n-1}x +(n-1)[\int cos^{n-2}xdx-cos^nxdx]$$
$$ = sinxcos^{n-1}x +(n-1)\int cos^{n-2}xdx-(n-1)\int cos^nxdx$$
but In = cosn xdx . hence
$$I_n =sinxcos^{n-1}x+(n-1)I_{n-2} -(n-1)I_n$$
$$I_n +(n-1)I_n=sinxcos^{n-1}x+(n-1)I_{n-2} $$
$$I_n +nIn_n-I_n=sinxcos^{n-1}x+(n-1)I_{n-2} $$
$$nIn=sinxcos^{n-1}x+(n-1)I_{n-2} $$
$$I_n = \frac{sinxcos^{n-1}}{n} +\frac{(n-1)I_{n-2}}{n} \ for \ n \geq 2 $$
when n = 5, our original equation becomes:
$$I_5 = \int cos^5xdx =\frac{sinxcos^4x}{5} + \frac{4}{5}I_3$$
but
$$I_3 = \frac{sinxcos^2x}{3} +\frac{2}{3}I_1 $$
whereas
$$I_1 = \int cosxdx = sinx +C $$
therefore
$$I_5 = \int cos^5xdx =\frac{sinxcos^4x}{5} + \frac{4}{5}(\frac{sinxcos^2x}{3}+\frac{2}{3}I_1)$$
$$I_5 = \int cos^5xdx =\frac{sinxcos^4x}{5} + \frac{4}{5}(\frac{sinxcos^2x}{3}+\frac{2}{3}sinx) +C$$
$$I_5 = \int cos^5xdx = \frac{sinxcos^4x}{5} + \frac{4sinxcos^2x}{15} + \frac{8sinx}{15} +c $$
obtain the reduction formula for
$$I_n = \int sin^nxdx$$
hence solve
$$ \int sin^4xdx$$
Expected Answers
$$I_n = \frac{-cosxsin^{n-1}x}{n} + \frac{(n-1)}{n} I_{n-2}, \ \ \ n \ \ \geq 2 $$
$$\int sin^4x = \frac{-cosxsin^3x}{4} – \frac{3}{8}cosxsinx + \frac{3}{8} +c $$
Please note:
$$I_o = \int 1 dx = x+c $$
obtain the reduction formula for the following integral:
$$I_n=\int tan^nxdx$$
solution
tann x can be written in terms of (tan(n-2) x)(tan2 x), hence:
$$\int tan^ndx = \int tan^{n-2}x(tan^2x)dx$$
but tan2 x = sec2 x-1, hence:
$$\int tan^ndx = \int tan^{n-2}x(sec^2x-1)dx$$
$$ = \int (tan^{n-2}xsec^2x – tan^{n-2})dx $$
Therefore
$$I_n = \int (tan^{n-2}xsec^x – \int tan^{n-2})dx $$
$$I_n = \int tan^{n-2}xsec^2xdx – I_{n-2} ———-(i)$$
Considering the integral:
$$\int tan^{n-2}xsec^2xdx$$
u = tann-2 x and dv = sec2 xdx
$$du = (n-2)sec^2xtan^{n-3}xdx $$
$$v = tanx$$
applying integration by parts:
$$tan^{n-2}sec^2xdx = tan^{n-1}x-(n-2)\int sec^2xtan^{n-2}xdx $$
but sec2 x=1+tan2 x, hence
$$tan^{n-2}sec^2xdx = tan^{n-1}x-(n-2)\int (1+tan^2x)tan^{n-2}xdx $$
$$ = tan^{n-1}x-(n-2)\int tan^2xdx -(n-2)\int tan^nx dx $$
therefore
$$\int tan^ndx = tan^{n-1}x – (n-2)I_{n-2} – (n-2)I_n $$
substituting:
$$I_n \ for \int tan^nx$$
$$I_n = tan^{n-1}x -(n-2)I_{n-2}-(n-2)I_n – I_{n-2}$$
$$I_n+(n-2)I_{n-2} = tan^{n-1}x – (n-1)I_{n-2} $$
$$(n-1)I_n= tan^{n-1}x – (n-1)I_{n-2} $$
In therefore becomes:
$$I_n=\frac{tan^{n-1}x}{n-1} – I_{n-2} , n \geq 2 $$
obtain a reduction formulae for :
$$I_n =\int cot^nxdx$$
Hints:
$$I_n = \int cot^nxdx = I_n =- \frac{cot^{n-1}x}{n-1} – I_{n-2} \ , n \geq 2$$
$$\int tanxdx =-ln|cosx| \ or \ ln|secx| $$
$$\int cosecx =tan\frac{1}{2}x = -ln|cosex+cotx| $$
Obtain the reduction formulae for:
$$I_n = \int sec^nxdx = \int sec^{n-2}xsec^2xdx$$
solution
Let u =secn-2 x
du = (n-2)secxtanxsecn-3 xdx
dv = sec2 x
v=tanx
$$I_n = tanxsec^{n-2}x – (n-2)\int tan^2xsec^{n-2}xdx$$
$$=tanxsec^{n-2}x-(n-2)\int tan^2xdx+(n-2)\int sec^{n-2}xdx$$
$$$$
$$I_n = tanxec^{n-2}x-(n-2)I_n +(n-2)I_{n-2}$$
$$(n-1)I_n = tanxsec^{n-2}x+(n-2)I_{n-2}$$
$$I_n = \frac{tanxsec^{n-2}x}{n-1} + \frac{(n-2)}{(n-1)}I_{n-2} $$
Obtain a reduction formula in:
$$I_n = \int cosec^nxdx$$
ANSWER
$$I_n = \frac{-cotxcosec^{n-2}x}{n-1}+\frac{n-2}{n-1}I_{n-2}, \ n \geq 2$$
mn The reduction formula for integrals of the form
$$I_mn = \int x^m(1-x^2)^n$$
is typically used to simplify integrals involving powers of x and terms like (1−x2 )n . These integrals often appear in the context of trigonometric integrals or in solving problems related to orthogonal polynomials like Legendre polynomials.
A standard reduction formula for this type of integral is:
$$I_{mn} = \int x^m(1-x^2)^ndx$$
The general form of the reduction formula for Imn is derived by applying integration by parts, or by using properties of Beta and Gamma functions, or by recursively reducing the degree of the polynomial. Here’s an example of a reduction formula:
$$I_{mn}= \int x^m(1-x^2)^ndx$$
This formula essentially relates the integral Im,n to simpler integrals by reducing the powers of xxx. The specific formula can vary depending on the values of mmm and n, and also the boundaries of the integral (whether it’s definite or indefinite).
Obtain the reduction formulae for
$$Obtain \ the \ reduction \ formulae \ for \ I_n = \int x^ncosxdx $$
let u = xn
dv = cosxdx
du = nxn-1 dx
v = sinx
$$I_n = x^nsinx -n\int x^{n-1}sinxdx ———–(i)$$
but
$$\int x^{n-1}sinxdx$$
u = xn-1 and dv = sinxdx
du = (n-1)xn-2 dx
v = cosx
$$\int x^{n-1}sinxdx = -x^{n-1} cosx + (n-1) \int x^{n-2}cosxdx $$
$$-x^{n-2}cosx + (n-1)I_{n-2} ———- (ii)$$
$$I_n = x^n sinx + nx^{n-1}cosx – n(n-1)I_{n-2} , n \geq 2$$
show that:
$$I_{m,n} = \int sin^mxcos^nxdx = \frac{-1}{m+n}sin^{m-1}xcos^{n+1} + (\frac{m-1}{m+n}I_{m-2}) \ for \ m,n \ge \ 2$$
solution
$$I_{m,n} = \int sin^mxcos^nxdx = \int sin^{m-1}x(cosxcos^nx)$$
let u = sinm-1 x
dv = sinxcosn xdx
du = (m-1)cosxsinm-2 dx
$$V = \frac{-1}{n+1}cos^{n+1}dx $$
$$I_{mn} = \frac{-1}{n+1}sin^{m-1}xcos^{n+1}x+\frac{m-1}{n+1} \int cos^{n+2}xcos^{m-2}dx$$
$$=\frac{-1}{n+1}sin^{m-1}xcos^{n+1}x+\frac{m-1}{n+1} \int sin^{m-2}xcos^nxcos^2xdx$$
$$=\frac{-1}{n+1}sin^{m-1}xcos^{n+1}x + \frac{m-1}{n+1}\int sim^{m-2}xcos^nx(1-sin^2x)dx$$
$$=\frac{-1}{n+1}sin^{m-1}xcos^{n+1}x+\frac{m-1}{n+1}\int sin^{m-2}xcos^nxdx – \frac{m-1}{n+1}\int sim^mxcos^nxdx$$
$$I_{mn} = -\frac{1}{n+1}sin^{m-1}xcos^{n+1}x+\frac{m-1}{n+1}I_{m-2}, n-\frac{m-1}{n+1}I_{mn}$$
$$I_{m,n}+\frac{m-1}{n+1}I_{mn} = \frac {-1}{n+1}sin^{m-1}xcos^{n+1}x + \frac{m-1}{n+1}I_{m-2},2$$
$$\frac{m+n}{n+1}I_{m,n} = \frac{-1}{n+1}sin^{m-1}xcos^{n+1}x + \frac{m-1}{n+1}I_{m-2}, n$$
$$I_{mn} = \frac{-1}{m+n}sin^{m-1}xcos^{n+1}x+\frac{m-1}{m+n}I_{m-2} \ , m \ge 2 $$
Find the reduction formula for :
$$I_n = \int x^ne^xdx \ hence \ evaluate \ I_3 = \int x^3e^xdx$$
hint:
$$I_n = x^ne^x-I_{n-1} \ , n \ge1$$
2.
show that:
$$I_n= \int (lnx)^ndx = x(lnx)^n – nI_{n-1} , n \ge1$$
3. Find the reduction formulae for :
$$I_n = \int x^ne^{-x^2}dx$$
hint:
$$I_n =\frac{1}{2}x^{n-1}e^{-x^2}+(\frac{n-1}{2}I_{n-2})\ , \ n\ge2$$
4. obtain the reduction formulae for :
$$I_{m,n} = \int x^m(lnx)^ndx$$
hint:
$$I_{m.n} = \frac{x^{m+1}}{m+1}(lnx)^n – (\frac{n}{m+1})I_m \ , (n-1) $$
Use Integration by parts to complete the following integrals:
1.
$$\int xe^2xdx$$
2.
$$\int tsintdt$$
3.
$$\int xcos3xdx$$
4.
$$\int x^3lnxdx$$
5.
$$\int \sqrt{y} \ lnydy$$
6.
$$\int (lnt)^2dt$$
7.
$$x^2tan^{-1}xdx$$
8.
$$\int sec^{-1}(\sqrt{x})dx$$
9.
$$\int tan^{-1} \ \sqrt{x}dx$$

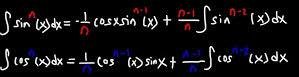

Leave a Reply