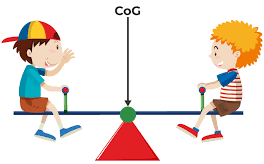
The center of gravity (CG) of an object is the point where its entire weight can be considered to act. It is the average location of the weight distribution of an object. In simple terms, it’s the balance point of the object.
Explaining Center of gravity
An object is considered to be made up very many particles that are joined together to form the whole object.
Each particle in an object experiences gravitational attraction.
The figure below illustrates particles of solid experiencing gravitational attraction. Each particle will have weight w assuming that all the particles are of same mass.

Gravitational attraction is the force between two bodies of given mass.
Any object or particle that has some mass will be attracted towards the center of the earth. The force of attraction on any particle or object of mass m by Earth’s attraction on it is given as w=mg.
This force on an object by the earth’s gravitational force is the weight of the object.
The weight of all the particles in the object sums up to provide the weight of the object. The sum of these gravitational attractions on all particles of an object acts through one point in an object called centre of gravity.
The figure below illustrates a straight metal rod with tiny particles experiencing some gravitational pull.

if moments were taken about point o, such that the sum of moments about it from the left or right of o balances, then the straight rod will balance at o without toppling. Point o is then said to be the centre of gravity of the metal rod.
The centre of gravity of a body is defined as the point of application of the resultant force due to earth’s attraction on the body.
some books defines center of gravity as a point on a body or system where force of gravity can be considered to act. It is the point in any object about which the object is in perfect balance no matter how it is turned or rotated around that point.
Most often, the center of gravity of bodies with a regular shape is also the geometrical center of that body. The mass of such a body is said to be uniformly distributed. For Example when we cut a straight metal rod illustrated earlier into pieces of equal length, then each piece cut will be having equal mass and consequently, the mass of the straight rod is proportional to it’s length.
The center of gravity of an irregular object is closer to the part that has more particles or where most of the mass is concentrated.
Center of gravity and the state of balance
A support placed at a point on the centre of gravity of an object places the object in a state of balance so that it does not turn or tip. This is because the weight of an object acts through the center of gravity of an object.
If a pivot is some distance from the center of gravity of an object, the object tips off in the direction of the weight, this is because the weight of an object causes the turning effect to a pivoted object.
Example question on Center of gravity
A uniform metal bar 160 cm long is pivoted at 30 cm mark such that it balances when a mass of 2.0 kg is attached at 0 cm mark as shown in figure 4.5. Calculate the weight of the bar.(take g=10Nkg-1)

solution
This metal bar is a uniform body and so it’s mass is evenly distributed, therefore it’s weight will act at its geometrical center which is it’s center of gravity . The weight will act at the 80 cm mark as shown because it is the center of the bar as shown.

The moments due to weight balances with moments due to the mass at the 0 cm mark on the metal road.
the distance from weight to the pivot =50 cm = 0.5 m
distance from 2.0kg mass from the pivot is 30 cm = 0.3 m.
the weight of the mass is 2.0kg x 10Nkg-1 = 20.0N
The clockwise moments will be given by W x 0.5 m
Anticlockwise moments will be given by 20.0 N x 0.30 m
from the principles of moments:
20.0 N x 0.30 m = W x 0.5 m
Exercise Problems
An object is pivoted such that it is balanced by a force of 4.0 N placed 70 cm from the fulcrum. If the weight of the object acts at 55 cm from the fulcrum on the opposite side,find the center of gravity of the object and it’s mass.
Answers:
- center of gravity is 125 cm from one end
- the mass is approximately 5.091 kg

Leave a Reply