A straight line is a one-dimensional geometric object that extends infinitely in both directions without curving or bending. It is the shortest path between any two points on the line and has a constant direction. Straight lines passes through some definite points that can be traced on a Cartesian plane. A point on a Cartesian plane is given as a combination of x and y coordinates. Equation of a straight line represents a function that maps points on horizontal axis to a matching point on vertical axis of a Cartesian plane where the line is passing.
A straight line can be considered to be a vector between two planes that are perpendicular to each other. consider a ladder attached to the a wall as shown.

The ladder is supported by two planes. The first plane is the floor surface and the second plane is the wall. If the top end of the ladder is raised to a higher position on the wall, the bottom end comes closer to the wall. We talks about steepness. A ladder is steep when its bottom is closer to the wall. The farther it is from the wall, the less steep it becomes. The steeper the ladder, the more difficult it becomes to climb. However, the climbing distance is shorter.
Gradient of a straight lines
Gradient is the steepness of the a line. In a Cartesian plane, a line is steep if it is closer to the vertical axis. It is less steep if it is closer to the horizontal axis.

The distance from the feet of the ladders to the wall are 3 m and 2 m respectively. If one uses the longer ladder he will cover (4/3) m vertical height for every 1 meter he moves horizontally. Similarly, when using the shorter ladder, he will need to move 1 m horizontally to rise by 2 m vertically.
in both cases, we can find the ratio of vertical distance to horizontal distance.
For shorter ladder, the ratio will be given by:
for the longer ladder:
From the calculations, the ratio is higher for the steeper ladder. The ratio of vertical distance to horizontal distance is known as the gradient.
For lines in Cartesian plane, gradient is the ration of vertical axis to the horizontal axis.
Consider the diagram below:
The gradient of the line will be given by ratio of move in y to move in x. that is;
consider the equation in the figure below:
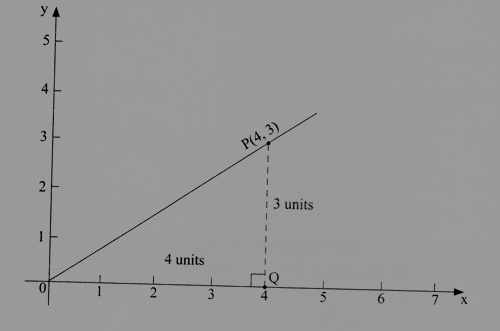
The vertical distance = 3 and the horizontal distance =4
the gradient of the line will be given by:

Leave a Reply