Integrating quadratic polynomials involves transformation the quadratic polynomial into a trigonometric expression which we can easily integrate. A quadratic polynomial is an algebraic expression of the form ax2+bx+c. It is a polynomial where the highest power is 2. Polynomials are algebraic expressions that consist of variables and coefficients.

consider the expression:
The best approach is ensuring that the quadratic polynomial is in the form of a perfect square.
The nearest perfect square to our quadratic polynomial is given by
(x+1)2 =(x+1)(x+1)= (x2+2x + 1)
(x2+2x + 1)+1 =x2+2x+2
thus x2+2x+2 = (x+1)2 +1
using the above to rewrite our integral we get:
then using trigonometric substitution, we have:
then differentiating x in terms of tanθ;
then we rewrite the integral:
From the above transformation, the quadratic expressions has been converted to a trigonometric expression.
tan2θ+1 = sec2θ
from the relation:
hence we have:
Example problems involving Integrating quadratic polynomials
- Evaluate
we need to express the given quadratic expression into a perfect square.
rewriting the expression 9 + 16x – 4x2 as – 4x2 + 16x +9
dividing by 4 to make coefficient of x2 to be 1;
-4(x2-4x-9/4)
we now complete the square by adding 1/2(-4)2 being careful not to change the value of the expression.
As you can see, we have added -2 squared and subtracted it immediately to ensure the expression value remains the same.
opening the brackets:
rearranging we have:
our integral is then transformed as follow:
The trigonometric substitution to be used in this expression is 2(x-2)=5sinθ
differentiating x with respect to sinθ:
hence substituting dx:
our integral then becomes:
from the trigonometric identities:
1-sin2θ = cos2θ, hence:
the expression under the square bracket is now a perfect square and we can get the square root. The expression thus becomes:
dividing by 5 and cosθ , the expression becomes:
from our substitution factor 2(x-2) = 5sinθ;
θ is thus the sine inverse of the above expression.
our working thus results to:
Revision Exercise
Problems
1.
2.
3.
4.
Answers
1.
2.
3.
4.
Related Topics
- Trigonometric substitutions: concise approach
- Introduction to heat conduction
- Fundamental Theorem of Calculus Examples and Solutions
- Basic Integration rules
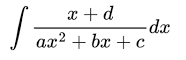

Leave a Reply