precisestudy

Integration by parts

Integration by parts-1: Excellent Concise approach

—

Integration by parts is a mathematical techniques to solve integrals that are composite of two or more functions.

Often in mathematics, a function can be as a result of two functions. For example

  • y1=3x+2 and
  • y2=5x-7

If we multiply y1 and y2, the product is a function that is a composite of two functions. that is :

y1y2 = (3x+2)(5x-7)=15x2-11x-14

consider the function y = cos x and g = 4x2

A composite function would be created from the two by the function:

yg=4x2cosx

General expressions of Integration by parts

let the function y=UV. We start by expressing the partial derivative of the function UV.

if U and V are both functions of x, the the derivative of UV will be given by.

$$\frac{d}{dx}UV = V\frac{du}{dx}+U\frac{dv}{dx}$$

we make V(du/dx) the subject:

$$V\frac{du}{dx} dx= \frac{d(UV)}{dx} -U\frac{dv}{dx}dx $$

Integrating the new expression:

$$\int V\frac{du}{dx}dx = \int \frac{d}{dx}(UV) – \int\ U \frac{dv}{dx} dx$$

integrating UV and rearranging:

$$\int U\frac{du}{dx} =(UV) – \int\ V \frac{dv}{dx} $$

then:

$$\int Udv = UV – \int Vdu $$

When working with partial integrals, we must choose what will be U. We also decide which function should be V. Our choice determines ease with which solve the function. Wrong choice of U and V can make it difficult to solve the problem. The following order should be observed.

  • Logarithmic function (L)
  • Inverse function (I)
  • Algebraic function(A)
  • Trigonometric function(T)
  • Exponential function(E)
  • constant(C)

The letters in the brackets can be combined to make the acronym LIATEC that can help us remember the order.

Example questions on Integrating by parts

  1. solve
$$\int xe^xdx$$

Solution

The integral is a product of two functions and so integration by parts could the best strategy

let u = x and V = ex

$$\frac{du}{dx}=1 \ and \ hence \ du=dx$$

similarly;

$$\frac{dv}{dx}=e^x$$

now consider the general integral:

$$\int Udv = UV – \int Vdu $$

we substitute both the function and their derivatives in the integral respectively:

$$\int xe^xdx = xe^x-\int e^xdx$$
$$\int e^xdx = e^x+C$$

hence:

$$\int xe^xdx = xe^x- e^x +C = e^x(x-1)+C$$

Example 2

$$\int xcosx dx$$

solution

we let u = x and v= sin x

$$\frac{dv}{dx} = cosx$$

substituting in the general integral:

$$\int x cosx dx = xsinx-\int sinx $$

but

$$\int sinx dx = cos x +C $$

hence:

$$\int x cosx dx = xsinx-cosx+C $$

Example 3

$$\int x^2 lnx dx $$

solution

in the order of LIATEC, we let the logarithmic function be substituted on u of the general integration by parts.

u = lnx and dv = x2dx

$$\frac{du}{dx} = \frac{1}{x} $$
$$du = \frac{dx}{x}$$

if dv = x2dx, then:

$$\int x^2lnx = \frac{x^3}{3}lnx – \int \frac{x^2}{3} \frac{dx}{x} = \frac{x^3}{3}lnx-\frac{1}{3}(\frac{x^2}{3})+c $$

hence:

$$= \frac{x^3}{3}lnx = \frac{x^2}{9} +C $$

Example 4

4.

$$\int e^xcosxdx$$

solution

let u = cosx

dv = exdx

du = -sinx dx

$$\int dv = \int e^xdx$$
$$ v = e^x$$
$$\int e^xcosxdx = e^xcosx + \int e^xsinxdx \ ———-(i)$$

you can see that the integration above has produced another integral that need to be integrated by part. we have named the first results of the integration as equation (i)

consider the integral in the result:

$$\int e^x sinxdx $$

we let :

u = sinx

dv = exdx

u = cosx dx

v = ex

$$e^xsinxdx = e^xsinxdx – \int e^xcosxdx ———(ii) $$

substituting (ii) in (i):

$$\int e^x cosxdx = e^xcosx + e^x sinx + C – \int e^x cosx dx$$

we add the integral on the right on both sides of the equation so that we have:

$$\int e^x cosxdx +\int e^x cosx= e^xcosx + e^x sinx + C – \int e^x cosx + \int e^x cosxdx$$

hence the integral to the right vanishes and we have

$$2\int e^x cosxdx= e^xcosx + e^x sinx + C $$
$$\int e^xcosxdx = \frac{e^xcosx}{2} +\frac{e^xsinx}{2} + C $$

Example 5

$$\int lnx dx$$

solution

u= lnx

dv = dx

v = x

$$ \frac{du}{dx} = \frac{1}{x} $$

substituting in the general integral by parts:

$$\int ln x dx = xlnx – \int dx $$
$$ = xlnx – x+C$$

Example 6

$$\int tan^{-1}dx $$

solution

let u = tan-1 x and dv = dx

$$v=x$$
$$\frac{du}{dx} = \frac{1}{1+x^2}$$
$$du = \frac{dx}{1+x^2}$$

substituting in the general integral:

$$\int tan^{-1} dx = x tan^{-1} – \int \frac{x}{1+x^2} dx $$

looking inside the integral on the right hand side:

$$u = 1+x^2$$
$$\frac{du}{dx} = 2x $$
$$du = 2xdx$$

Therefore:

$$dx = \frac{du}{2x}dx$$
$$\int \frac{x}{1+x^2} dx = \int \frac{x}{u}\frac{du}{2x} = \int \frac{du}{2u} = \frac{1}{2}\int\frac{du}{u}$$
$$=\frac{1}{2}lnu+C=\frac{1}{2}ln|1+x^2|+C$$

Therefore:

$$\int tan^{-1} dx = x tan^{-1}-\frac{1}{2}ln|1+x^2| +C$$

summary Remarks

Integration by parts is a technique used to solve integrals, particularly when the integrand is a product of two functions. It’s based on the product rule for differentiation and is derived from the following formula

$$∫u(x)v′(x) dx=u(x)v(x)−∫v(x)u′(x) dx $$
$$ = u(x) v(x) – \int v(x) u'(x) \, dx=u(x)v(x)−∫v(x)u′(x)dx$$

Related pages

Discover more from precisestudy

Subscribe to get the latest posts sent to your email.

Comments

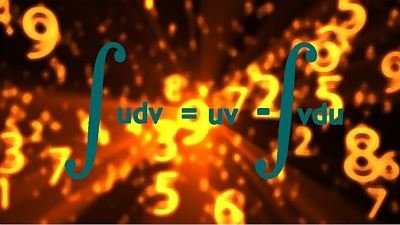
Leave a Reply

Your email address will not be published. Required fields are marked *

Discover more from precisestudy

Subscribe now to keep reading and get access to the full archive.

Continue reading