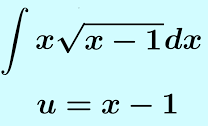
In Calculus, Integration by substitution is when we replace an integral value or its parts in an attempt to make the expression easier to integrate.
Consider the function f(u) such that u is a function of x.
let u = f(x) and f(u)=u
$$ \frac{\mathrm{d} }{\mathrm{d} x}f(u) = \frac{\mathrm{du} }{\mathrm{d} x}f'(u)$$
where:
$$f'(u) = \frac{\mathrm{d} f(u)}{\mathrm{d} u}$$
Integrating….;
$$\int \frac{\mathrm{d} u}{\mathrm{d} x}f'(u)dx = \int \frac{\mathrm{d} } {\mathrm{d} x} f(u)dx = f(u) + C$$
but:
$$f'(u) = {\frac{\mathrm{d}f(u) }{\mathrm{d} u}}{}$$
so that
$$\int f'(u)du = f(u) + c$$
$$\int \frac{\mathrm{d} u}{\mathrm{d} x}f'(u)dx = \int f'(u)du = f(u) + C$$
Example 1
Solve the problem below using Integration by substitution:
$$\int x^{2}\sqrt{x{^{3}+5}}$$
solution
substitute the expression under the root sign as shown:
let
$$ u ={x{^{3}+5}}$$
then integrating u with respect to x we get:
$$\frac{\mathrm{d} u}{\mathrm{d} x} = 3x^{2}$$
and so:
$$du = 3x^{2}dx$$
and making dx the subject:
$$dx = \frac{\mathrm{d} u}{\mathrm{3} x^{^{2}}}$$
rewriting the expression:
$$$$
$$\int x^{2}\sqrt{x{^{3}+5}} = \int x^{2}\sqrt{u} \frac{\mathrm{du} }{\mathrm{3} x^{2}} $$
x2 on the numerator can then be cancelled out by the x2 on the denominator.
The expression becomes:
$$\int \frac{\sqrt{U}{du} }{\mathrm{3} x^{^{2}}} = \int \frac{\mathrm{u} ^{\frac{\mathrm{1} }{\mathrm{2} }}}{\mathrm{3} } du$$
=
$$ = \frac{1}{3}\int U^{^{^{\frac{1} { 2}}}} du$$
$$\frac{1}{3}. \frac{U^{\frac{3}{2}}}{\frac{3}{2}} + C = \frac{2U^{\frac{3}{2}}}{9} + C$$
$$\frac{1}{3}. \frac{U^{\frac{3}{2}}}{\frac{3}{2}} + C = \frac{2U^{\frac{3}{2}}}{9} + C =\frac{2}{9}(x^{3}+5)^\frac{3}{2} +C$$
Example 2
solve :
$$\int 2x\sqrt{1+x^{2}} dx$$
solution
let u = 1 +x2
then differentiating u with respect to x
$$\frac{du}{dx} =2u$$
and then rearranging:
$$dx= \frac{du}{2x}$$
then rewriting the integral:
$$\int 2x \sqrt{u} \frac{du}{2x} = \int \sqrt{u} du$$
2x on the denominator has cancelled the 2x on the numerator so that we only have u that is easy to integrate:
$$\int \sqrt{u} du = \int u^{\frac {-1}{2}} du = \left[ \frac{u^{\frac{3}{2}}}{\frac{3}{2}} +C \right]$$
$$=\frac{2u^{\frac{3}{2}}}{3} + C = \frac{2(1+x{^{2}})^{\frac{3}{2}}}{3} + C$$
Example
solve by substitution:
$$\int \frac{1}{\sqrt{2x+1}} dx$$
solution
let u = 2x + 1
differentiating u with respect to x we obtain;
$$\frac{du}{dx} = 2$$
now we express dx in terms of u as:
$$du = \frac{dx}{2}$$
Then we need to rewrite our integral as:
$$\int \frac{1}{u^{\frac{1}{2}}} \frac{du}{2} = \frac{1}{2} \int u{^{\frac{-1}{2}}}du$$
then:
$$ \int u{^{\frac{-1}{2}}}du =\frac{1}{2} [\frac{u^{\frac{1}{2}}}{\frac{1}{2}}] + C
$$
$$=U^{\frac{1}{2}} + C$$
rem U = 2x + 1
and any number raised to power of 1/2 is like finding it’s squareroot
hence:
$$ U^{\frac{1}{2}} + C = \sqrt{2x + 1} + C$$
substitution Problem involving trigonometric ratios
solve:
$$ \int cosxsin^3x dx$$
solution:
let u = sin x: then
$$\frac{du}{dx} = cos x $$
$$dx = \frac{du}{cosx}$$
and applying substitution in our integral, we replace dx;
$$\int cosxsin^3x dx = \int cosx . u^3\frac{du}{cosx}$$
cos x in the numerator cancels the one at the denominator that the expression is reduced to:
$$\int u^3du$$
$$\int u^3du =\frac{U^4}{4} + C$$
but u = sin x; therefore:
$$\frac{U^4}{4} + C = \frac{sin^4x}{4} + C$$
generally:
$$\int cosxsin^xx dx = \frac{1}{n+1} sin^{n+1} +C$$
Example on trigonometric substitution
solve:
$$\int sinxcos^5xdx$$
solution
let u = cos x
$$du = -sin x dx$$
$$\frac{du}{-sinx} = dx$$
rewriting dx in our original integral:
$$\int sinxcos^5xdx = \int sinxcos^5x\frac{du}{-sinx}$$
we eliminate sin x in the integral to obtain the following expression:
$$=\int -cos^5xdu$$
but cos x = u
hence cos5x = u5 and so the integral becomes:
$$- \int u^5du$$
hence we get:
$$- \int u^5du = -\frac{u^6}{6} + 6$$
and then replacing u for cos x we get:
$$- \frac{cos^6 x}{6}+C$$
in general:
$$\int sinxcos^nxdx = \frac{-1}{n+1}cos^{n+1} x+ C$$
Integration by substitution: natural log by substitution
solve:
$$\int \frac{ln x}{x}dx$$
solution
let u = lnx
$$\frac{du}{dx} = \frac{1}{x}$$
x du = dx
hence we write the integral as:
$$\int \frac{ln x}{x}dx = \int \frac{lnx}{x}x du$$
and so we eliminate x to have the integral:
$$\int lnxdu = \int udu$$
$$ \int udu = \frac{u^2}{2} + C = \frac{(lnx)^2}{2} + C $$
Example on sec trigonometric ration
solve:
$$\int sec^2(3x-1)dx$$
solution
let u = 3x-1
$$\frac{du}{dx} =3 $$
du = 3dx
$$dx = \frac{du}{3}$$
$$\int sec^2u \frac{du}{3} = \frac{1}{3} \int sec^2udu = \frac{1}{3}tan u + c = \frac{1}{3}tan(3x-1)+C$$
Example 3 on trigonometric ratio
integrate:
$$\int sin xe^{cosx} dx $$
solution
let u = cos x
$$du = -sinxdx$$
$$dx = \frac{du}{-sinx}$$
$$= \int sinx e^u \frac{du}{-sinx} = -\int e^udu = -e^u+c$$
Practice exercise
use the substitution method to evaluate the following integrals:
1. $$\int x (x^2-3)^4dx$$
2. $$\int x \sqrt{1-x^2} dx $$
3. $$\int cos 2x(sin(2x+3))^2 dx$$
4. $$\int e^x \sqrt{1+e^x} dx$$
5. $$\int sec^2xtan^2xdx$$
6. $$\int \sqrt{x}\sqrt{1+x^{\frac{3}{2}}}dx$$
7. $$\int(x+1)sin(x^2+2x+2)dx$$
8. $$\int (x+1)\sqrt{x^2+2x+3}dx$$
9. $$\int \frac{x^2}{(x^3+8)^4}dx$$
Related Topics

Leave a Reply