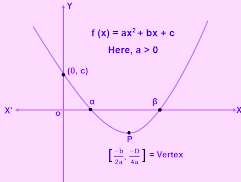
Quadratic equations is any equation of the form ax2+bx+c=0 where a is not zero. In other words, quadratic equation is a quadratic expression that is equated to a zero as a value.
solving quadratic equations
methods of solving quadratic equations includes:
- factorization which involves rewriting the equation as a product of two binomials.
- completing the square which involves rewriting the equation into a perfect square form.
- the quadratic formula which is a method that is useful when the first two method cannot be work.
solving Quadratic Equations by factorization
consider the quadratic equation: x2+3x-54 = 0.
we find two integers such that their products is -54 or their sum is +3. These numbers are -6 and 9.
-6+9 = +3
then we will replace 3x with -6x + 9x and rewrite the equation as shown:
x2-6x+9x-54 = 0.
we now have four terms in the expression and we can group them into twos.
(x2-6x)+(9x-54 )= 0
There is a common factor in each of the parenthesis.
x(x-6)+9(x-6) = 0
we have now two brackets with a similar expression. We join the factored values and then multiply with one of the parenthesis.
(x+9)(x-6) = 0
this tells us that: x+9=0 or x-6=0
therefore: x= -9 and x=6
therefore the solution to the quadratic equations are (6, -9).
the solution is known as the roots of the quadratic equation.
Related topics
- Quadratic expressions and equations: concise Introduction
- The equation of a circle
- Set Notations
- Operations on set
- Venn Diagrams
- Cardinality In sets
- set Identities

Leave a Reply