Quadratic expressions and equations: concise Introduction 1

Quadratic expressions are algebraic expressions of the form ax²+bx+c where a, b, and c are constants and a!=0. Constants means real numbers.

if a=0, the expression would be linear rather than quadratic. When a graph of a quadratic expression is plotted against x ,is a parabola is formed.

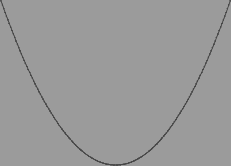
If a is greater than 0, the curve opens upwards as shown.

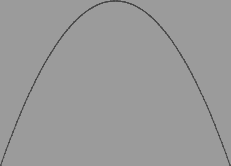
If a is less than zero, the curve opens downwards as shown.

examples of quadratic expressions is like:

• 5x² + 4x – 3
• x² + 2x – 1
• -3x² + 4x +10

Expanding algebraic expressions

Expanding algebraic expressions involves removing parentheses and simplifying the expression by multiplying terms and summing the like terms. Expansion makes use of the distributive property of algebra which states that a(b+c)=ab+ ac

consider the product of (x + y) and (a + b). The product can be written as (x + y)(a + b). if we let (a + b) = k, then we have kx + ky.

this can be expanded to:

(a + b) x + (a+ b) y = ax + bx + ay + by

From the illustrations above, one can see that each term in the first bracket is multiplied by each term in the second bracket.

Example 1

Expand : (4x + 5)(4y + 10)

solution

each term in the first bracket is multiplied by every term in the second bracket. so we have:

4x(4y + 10 ) + 5 (4y + 10) = 16xy +40x + 20y +50

Example 2

Expand (6a – 3) (4b + 7)

solution

(6a – 3) (4b + 7) =6a(4b + 7) -3 (4b + 7) = 24ab + 42a – 12b – 21

Example 3

Expand:

solution

Quadratic expressions

Quadratic expression is an algebraic expression where the highest power is 2. Most common quadratic equations has three terms which are usually referred to as quadratic terms. The term with a power of 2 is known as the quadratic term. The term with power of one is known as the linear term. The term with power of zero in the variable is known as the constant term.

consider the quadratic expression 3x²+7x +23.

3x² is the quadratic term, 7x is the linear term while 23 is the constant term.

A quadratic expression must have the quadratic term which should be the term with the highest power of the variable.

practice problem

State why each of the following is not a quadratic expression.

• 5x-1
• 4x³ + 7x² +3x + 15
• 6x⁴ + 5x³ + 3x² +11x +18

Example 4

Expand and simplify each of the following:

(a) (3x – 4)(2x + 1)

(b) (2x – 7)(x-8)

(c) (3k – 2)(k-7)

solution

(a)

(b)

(c)

The quadratic identities

Quadratic identities are formulas or equalities that hold true for all values of the variable. These identities are useful for simplifying expressions and solving equations. Some of the most important quadratic identities include:

1. (a + b)²= a² + 2ab + b²
2. (a – b)²= a² – 2ab + b²
3. (a + b)(a-b) = a² – b²

we will prove each of the above identities in the next sections.

1. The Square of a Binomial

consider the expression: (a+b)(a+b)

we establish that: (a+b)(a+b) = (a+b)²= a² + 2ab + b² in all cases.

consider the square below:

The square has sides of (a + b) units. It is divided into 4 parts A, B , C and D. A is a square of side length a units while D is a square of side length b units.

B is a rectangle of length a units and width b units. C is a Rectangle of sides a and b.

The area of the whole square = (a +b)²

Area of A = a².

Area of B = ab

Area of C = ab

Area of D = b²

The total area of the square with sides (a + b) will thus be:

a² + ab + ab + b²

2. The Difference of Squares

This identity expresses the difference of two squares as a product of binomials: That is a²−b²=(a+b)(a−b)

Related topics

• Equations of a straight line
• The Cartesian plane
• The equation of a circle