Tangent of an angle

Tangent of an angle is a ratio of two sides of a right angled triangle. It is one of the trigonometric ratios. Trigonometric ratios expresses an acute angle formed in a triangle as the ratio of the two sides out of three that makes a triangle.

Consider a triangle ABC shown below.

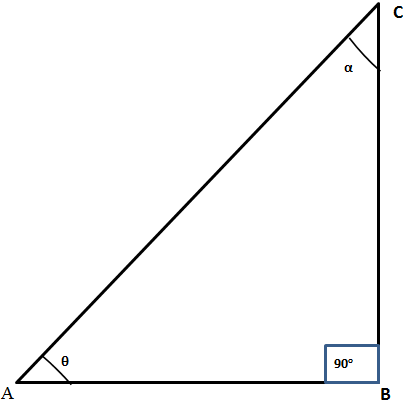
The triangle is a right angled triangle because one of it’s sides is 90^o. Angle ABC is 90^o and is usually represented by a small rectangle as in figure above. Right angled triangle is a triangle whose two shortest sides meets at 90^o. Angle θ is sited on line AB and it faces line BC. AB is referred as the adjacent side of Angle θ because the θ lies on it. Side BC is known as the opposite side of angle θ because θ directly faces it.

Similarly, angle α is sitting on line BC and is directly opposite side AB. BC is therefore the adjacent side to angle α while AB is the opposite side to angle α.

Tangent ratio is a ratio that compares length of the opposite side to the length of the adjacent side.

tangent of an angle is therefore expressed as :

Tangent ratio can be expressed as tan while opposite side is represented by letter O and the adjacent side represented by letter A. Therefore, if we have an angle θ opposite to side O and adjacent to side A, we express the tangent ratio in short form as:

Consider the figure below. There are many triangles but all of the sharing the same angle.

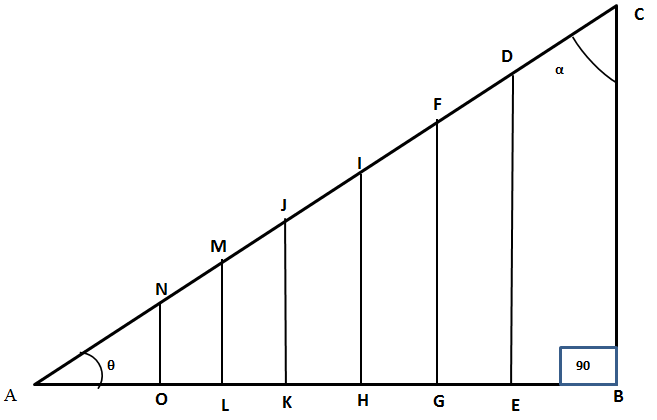
It can be shown that:

The constant is the tan ratio of the common angle θ.

By definition, the tangent of a given angle is the ratio of the opposite side to the adjacent side. That is:

Exercise involving tangent ratio

Express tan θ as a fraction in the figure below

Solution

practice question

Study the triangle below an express the angle θ as a tan ratio leaving your answer as a fraction.

Related topics

• The equation of a circle
• Angular Velocity
• Trigonometric substitutions
• Integrating trigonometric expressions

---