The equation of a circle is a fundamental concept especially in coordinate geometry. The equation represents all the points that are equidistant from a fixed point known as the center of a circle in a two-dimensional plane.
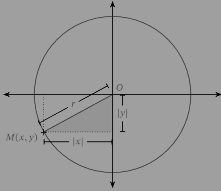
Consider a circle of radius r on a Cartesian plane centered at point o(a,b) as shown in figure below. A point p on the circumference of the circle has an arbitrary point (x, y).

line OQ an QP makes a right angle triangle with the radius r of the circle such OP=r, OQ = x-a and QP=y-b.
using Pythagoras’ theorem: (x-a)2 + (y-b)2 = r2.
Hence the general equation of a circle is given as:
(x-a)2 + (y-b)2 = r2.
where:
- r is the radius of the circle
- (a, b) are the coordinates at the center of the circle
- (x, y) is an arbitrary point on the circumference of the circle.
The equation of a circle problems
Find the equation of a circle centered at (4, 5) and with radius of 3 units.
Solution
Recall the equation: (x-a)2 + (y-b)2 = r2
a=4, b=5, r=3
hence (x-4)2+(y-5)2 = 32
=x2– 4x- 4x+ 16+ y2– 5y- 5y + 25= 9
x2-8x + 16 + y2 – 10y + 25 = 9
x2– 8x + y2– 10y+ 41=9
x2 – 8x + y2 – 10y + 32=0
Example problem
Find the equation of a circle given the center of the circle in the Cartesian plane and radius in each of the following:
(i) center : (0,2), radius = 3 units
(ii) center: (-5, -3), radius = 6 units
solutions
(i) taking an arbitrary point on the Cartesian plane: (x, y); we have:
hence equation of our circle on the Cartesian plane will be: x2 +y2-4y-5=0

Leave a Reply