precisestudy

Trigonometric substitutions illustrations

Trigonometric substitutions: concise approach

—

Trigonometric substitutions is a method for finding antiderivatives of functions. This method is used when the functions contain square roots of quadratic expressions. It is also applicable for rational powers of the form n/2 where n is an integer.

trigonometric ratios includes:

  • sine ratio
  • cosine ratio
  • tangent ratio
  • secants ratio
  • cosecant ratio
  • cotangent ratio

we express sine of an angle θ sinθ.

Similarly, the tangent of an angle is written as tanθ. The cosine ratio is written as cosθ. The secant ratio is written as secθ. Lastly, the cotangent ratio is written as cotθ.

let x = asinθ.

squaring on both sides we get: x2 = a2sin2θ

we rewrite this as: x2 – a2sin2θ = 0

if we happen to have an integrals in the form

$$\sqrt{a^{2} – x^{2}}$$

Then we use the substitution x = asinθ.

if we have the integral :

$$\sqrt{a^{2} + x^{2}}$$

then we use the substitution x = a tanθ.

when we have the integral:

$$\sqrt{x^{2} – a^{2}}$$

then we use the substitution of x = secθ.

Example problem in trigonometric substitutions

Evaluate:

$$\int\sqrt{4-x^{2}}dx$$

solution:

from our previous definitions; a2 = 4 and so a = 2.

from x = asinθ therefore, x = 2sinθ

$$\frac{dx}{dθ} = 2cosθ$$

hence dx = 2cosθdθ

rewriting the integral:

$$\int(\sqrt{4 – 4sin^{2}}θ)2cosθdθ = \int\sqrt{(4({1 – sin^{2}θ}})2cosθdθ$$

but sin2θ + cos2θ = 1

cos2θ = 1 – sin2θ

hence:

$$\int\sqrt{(4({cos^{2}θ}})2cosθdθ = \int2cosθ2cosθdθ = \int4cos^2θdθ$$
$$$$

but

$$cos^2θ = \frac{cos2θ+1}{2}$$

hence:

$$\int4cos^2θdθ = \int4(\frac{cos2θ+1}{2})dθ=\int2(cos2θ+1)dθ = 2\int(cos2θ+1)dθ$$

hence

$$=2\int cos2θdθ + \int2dθ$$
$$2\frac{sin2θ}{2}+2θ+C = sin2θ+2θ+C$$

remember:

x = 2sinθ

$$\frac{x}{2} = sinθ$$

from the trigonometric ratios;

sine of an angle θ can be determined from:

$$sinθ = \frac{opposite}{Hypotenuese}$$

from the Pythagoras theorem:

b2 + x2 = 22

b2 = 4 – x2

hence:

$$b = \sqrt{4 – x^{2}}$$

The angle θ can then be determined from the expression:

$$\theta=sin^{-1}\frac{x}{2}$$

The angle can be determined from cosine ratio as:

$$θ = cos^{-1}\frac{4-x^{2}}{2}$$

We can also determine the angle from tan ratio as:

$$\theta = tan^{-1}\frac{x}{\sqrt{4-x^2}}$$

remember that tanθ = opposite/adjacent.

Therefore θ = tan inverse of opposite/adjacent

Example 2 on Trigonometric substitution

evaluate:

$$\int\frac{1}{\sqrt{9-4x^2}}dx$$

solution

from the expression 9-4x2 : we substitute 2x=3sinθ

x = 3/2 sinθ

differentiating x with respect to sinθ we get:

$$dx = \frac{3}{2}cosθdθ$$

our expression is transformed as follow:

$$\int\frac{dx}{9-x^2} = \int\frac{\frac{3}{2}cos\theta d\theta}{\sqrt{9-9sin^2\theta}}=\int\frac{\frac{3}{2}cos\theta d\theta}{\sqrt{9(1-sin^2\theta)}}$$

but from trigonometric identities:

1-sin2θ = cos2θ

so in the square root expression, the expression is simplified as follow:

$$\int\frac{\frac{3}{2}cos\theta d\theta}{\sqrt{9(cos^2\theta)}}$$

The new expression becomes:

$$\int\frac{\frac{3}{2}cos\theta d\theta}{3cos \theta}=\int\frac{\frac{3}{2}\del{cos\theta}) d\theta}{3\del{(cos \theta}})$$

cosθ will cancel out in the expression so that we finally have

$$\int\frac{\frac{3}{2}}{3}d\theta = \int\frac{1}{2}d\theta = \frac{1}{2}\int d\theta$$

Integrating the angle θ then gives:

$$\frac{1}{2}\theta +c $$
$$=\frac{1}{2}sin^-1(\frac{2x}{3}) + C$$

Example 3 of Trigonometric substitution

Evaluate:

$$\int\frac{dx}{4\sqrt{9+x^2}}$$

Solution

from the expression 9+x2 , we get the square root of x and 9 so that we write:

x = 3tanθ

differentiating x with respect to tanθ;

$$\frac{dx}{dθ} = 3sec^2θ$$

hence we write derivative of x in terms of derivative of θ

$$dx =3sec^2θdθ$$

rewriting the integral and replacing the dx with derivative of tanθ and also x with 3tanθ in the square root terms:

$$\int\frac{3sec^2θdθ}{4\sqrt{9+9tan^2θ}}=\int\frac{3sec^2θdθ}{4\sqrt{9(1+tan^2θ)}}$$

but 1 + tan2θ = sec2θ

hence:

$$\int\frac{3sec^2dθ}{4\sqrt{9+9tan^2θ}}=\int\frac{3sec^2dθ}{4\sqrt{9(sec^2θ)}}=\int\frac{3sec^2dθ}{4(3)(secθ)}=\int\frac{sec\theta d\theta}{4}$$

And after integrating the simplified expression, we find :

$$\frac{ln|sec\theta+tan\theta| + c}{4}$$

from the expression: x = 3tanθ and remembering tan ratios;

$$tan\theta = \frac{x}{3}$$

consider the triangle below:

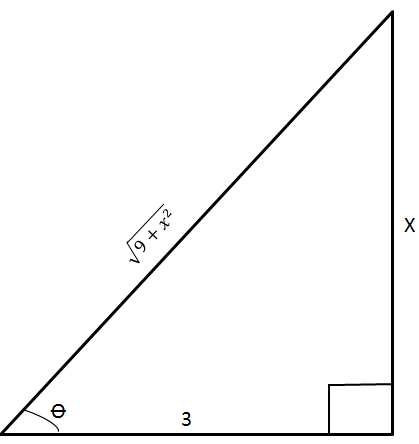
from the triangle:

$$cosθ = \frac{3}{\sqrt{9+x^2}}$$

but remember:

$$secθ = \frac{1}{cosθ} = \frac{\sqrt{9+x^2}}{3}$$

Hence:

$$\frac{1}{4}ln|\frac{\sqrt{9+x^2}}{3} + \frac{x}{3} |+ C$$

Revision Exercise

$$\int\frac{dx}{x\sqrt{9+x^2}}$$

answer:

$$-\frac{1}{3}ln|\frac{\sqrt{x^2+9}}{3} + \frac{x}{3}| +C$$

2.

$$\int \frac{dx}{\sqrt{16-x^2}}$$

Answer

$$sin^{-1}(\frac{x}{4}) + C $$

3.

$$\int\frac{1}{x^2\sqrt{4-x^2}}dx$$

Answer:

$$\frac{4-x^2}{4x} + C $$

4.

$$\int_{}^{}\frac{1}{\left( 9-16x^{2} \right)^{\frac{3}{2}}} dx$$

Answer

$$\frac{x}{9\sqrt{9-16x^2}} +C$$

5.

$$\int\frac{\sqrt{x^2-1}}{{x^2}} dx$$

Answer

$$ln|x + \sqrt{x^2-1}| – frac{\sqrt{x^2-1}}{x} +C$$

6.

$$\int x^3\sqrt{9+4x^2}dx$$

Answer

$$\frac{1}{80}[(9+4x^2)^{\frac{5}{2}} -15(9+4x^2)^{\frac{3}{2}}] + C$$

7.

$$\int \frac{x^2}{\sqrt{25-x^2}}dx$$

Answer

$$\frac{25}{2}sin^{-1}\frac{x}{5}-\frac{1}{2}x\sqrt{25-x^2}+C$$

Related Topics

Discover more from precisestudy

Subscribe to get the latest posts sent to your email.

Comments

Leave a Reply

Your email address will not be published. Required fields are marked *

Discover more from precisestudy

Subscribe now to keep reading and get access to the full archive.

Continue reading