The quantum theory of light proposes that light travels in bundles of energy, known as a photon. In 1909, Max Plank proposed that light energy is propagated as a small packets of energy that are discrete. Each packet of energy is referred to as a quantum of energy. The discrete amount of energy are called photons and posses a definite energy that can be determined from the frequency of the light waves.
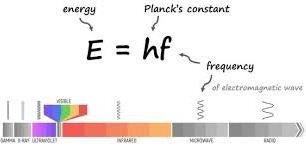
Energy E of a photon can be determined from the relation E=hf. Here, h is a constant value known as Plank’s constant. Max Plank introduced it in his theory.
Plank’s constant h is given as h=6.63 X 10-34Js
From the general equation of a wave:
where λ is the distance between two particles in a wave usually referred to as the wavelength.
expressing f in terms of speed of light:
substituting for f in the equation E=hf;
c is the speed of an electromagnetic radiation in vacuum and is given as
3.0 x 108ms-1
c and h are constants in the equation and so energy of a wave is only determined by the wavelength. From the equation, energy increases when wavelength reduces.
Energy of a photon is therefore inversely proportional to the wavelength.
Example problem on the Quantum theory
compare energy contained in a photon of red light of wavelength 6.7 x 10-7 m and violet light of wavelength 3.4 x 10-7m. (take Plank’s constant as 6.63 X 10-34Js)
solution
The energy carried by the red light will be given as :
c=3.0 x 108ms-1
substituting values in the equation:
Therefore energy carried by red light photon will be:
E = 2.9687 X 10-19 Joules
similarly for the violet light;
substituting values in the equation:
Therefore energy carried by red light photon will be:
E = 5.85 X 10-19 Joules
As can be determined from the above working, violet light has more energy compared to red light as it has shorter wavelength.
Light energy in a Photons
Most of waves are considered continuous and progress as in figure below:

A continuous wave can carry any amount of energy depending on the amplitude and frequency. There is no minimum energy of the wave but energy may be reduced simply by decreasing amplitude of the wave.
Quantum theory however shows that electromagnetic waves travels as wave packets also known as photons that are imagined to travel as shown.

Each photon carries a definite amount of energy that is proportional to the frequency of the radiation.
Example problem
Determine an energy carried in a photon of an x-ray with a frequency of 8.0 x 1017 Hz.
solution
Energy E = hf
=5.304 X 10-16 J
Threshold Frequency
Radiations below certain frequencies does not eject electrons from a metal surface no matter how intense the light will be.
The minimum frequency needed for a wave so that it is able to eject an electron from a metal surface is known as the threshold frequency fo.
If the frequency is below a certain value, it will be absorbed by the metal surface onto which it falls but no electron will be ejected to the surface.
Threshold wavelength
if the threshold frequency is fo ,the speed of the wave can be determined by:
c= foλo where λo is known as the threshold wavelength that corresponds with the threshold frequency. It is the maximum wavelength beyond which an electron wont be ejected from a metal surface.
in other words:
Work Function
The work function wo is the minimum amount of energy needed to eject an electron from a metal surface. It represents work that need to be done in order to remove a negatively charged electron from a metal atom by overcoming the force of attraction of the positively charged nuclei of the atom.
Different atoms have different magnitude of attractive forces between its nucleus and the electrons. This means different energy will be required to eject electrons from different metal surfaces. Therefore, the value of work function differs from one metal to another.

Leave a Reply