Reading meter Rule with accuracy

Table of Contents

A ruler is a tool mostly used to measure small lengths. A metre rule has a length of one metre, which is equal to one hundred centimeters.

A ruler, also known as a rule, scale and sometimes a line gauge, is an instrument used to measure lengths. A user estimates a given length by reading from a series of markings called rules along an edge of an object whose measurements are required. Mostly it is a rigid straightedge which allows one to draw straight lines.

Reading a meter rule with accuracy is often an underrated skill that can make a difference in experimental physics. Most of people don’t read meter rule correctly. A meter rule has 100cm and between two consecutive centimeter marks there are gaps. The gaps between centimeter marks can be reduced by dividing the gap into smaller sub units. When divided into 10 equal divisions, then each of such smaller division is called a millimeter because it will be dividing the meter length into 1000 divisions with each divisions being equal to 0.001m. Then the accuracy of the meter rule can be said to be equal to 1/1000 of a meter(0.001m).

That is:

$$\frac{1}{1000} = 0.001m$$

when the rule is calibrated into centimeter divisions alone, then the meter length is divided into 100 divisions with each divisions being equal to 0.01m. the accuracy of the measurements taken by such a rule is thus (1/100)m=0.01m).

accuracy in reading a meter rule

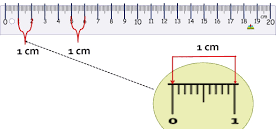
consider the reading shown by the arrow in figure below.

Illustrating reading of a meter rule — demonstrating reading of a meter rule

The reading above is more than 1.6 cm but less than 1.7 cm. The position of our point object is not lying on exact reading. we cannot precisely state what measurement it is because it is not indicated. there is an empty gap and we need to approximate that extra length beyond the 1.6 cm because it is not indicated. We can increase the accuracy of the meter rule by dividing the gap into smaller divisions. suppose we approximate the second decimal to be 1.65 cm, there is nothing that prevents us from stating it as 1.66 cm,1.67 cm or even 1.64 cm.

The second decimal place cannot be accurately determined. Nevertheless, the readings from a meter rule may be written up to the second decimal place of a centimeter.

A reading like 2.584 cm cannot be taken by a meter rule. In later lessons, we will discuss how to increase the decimal places in measurement of length using other special instruments like micrometer screw-gauge.

If the readings of 3.6 cm and 7 cm are taken with a meter rule, then they should be written as 3.60 cm and 7.00 cm respectively. This is because a meter rule is calibrated to an accuracy of 0.01 m (100 divisions).

Maximizing Precision

you can use a meter rule to determine approximation of given length or you can use the rule to get accurate measurements.

Approximation – This includes estimating the length.
Using a standard measure(instruments)

Meter rules and half meter rules are used.
They are graduated in centimeters and millimeter.
They are made of wood, plastic or steel.

How to read a ruler

Reading measuring instruments at an angle can make us read incorrectly. To be able to read a ruler accurately and effectively, proceed as follows:

Put the zero (0) mark to coincide with the start of the object to be measured.
Look perpendicular to the edge end of the measurement taken
For accurate reading, always place your eyes vertically above the mark to avoid parallax. see figure 1.1 below

The figure below shows the correct measurement of length using metre rule:

correct measurement using a meter rule — figure 1.4: using a meter rule correctly

Errors associated with measuring with a ruler includes:

The end of the object is not aligned to the zero mark of the meter rule scale as shown.

Rule not aligned with the zero mark of the object — figure 1.2 : rule not aligned with the zero mark of the object

The rule is not in contact with the object

rule not in contact of the object — figure 1.3: rule not in contact with the object

The error that occurs when the position of the eye is not perpendicular to the scale is called parallax error

Practice Question

Record the readings indicated by P₁,P₂ and P₃ shown in the figure below.

question to practice reading a meter rule

Answer to practice question

P₁=69.50 cm (approximations done)
P₂=71.00cm
p₃=71.50cm

Practice Exercise

State the readings indicated by the arrows in the figures below