Simplifying surds refers to the process of simplifying expressions that involve square roots, cube roots, or other root symbols etc. to make them easier to work with or more compact. This often involves:
Removing Perfect Squares (or other perfect powers)
If the number under the square root or root is a perfect square (or other perfect power), simplify the surd by factoring out the perfect square. For example:
Simplifying the Radicand
If the number inside the root is not a perfect square, break it down into factors that include perfect squares and simplify the expression. For example:
Rationalizing the Denominator
When a surd appears in the denominator of a fraction, it’s common practice to multiply both the numerator and denominator by an appropriate value to “rationalize” the denominator (i.e., make the denominator free of surds).For example:
- can be simplified by multiplying both the numerator and the denominator by
In essence, simplifying surds makes mathematical expressions more manageable and easier to handle in equations or calculations.
To simplify expressions involving surds, we simply add or subtract coefficient of irrational factors that are alike. thus
To simplify surds, you want to express them in their simplest form typically by factoring out any perfect square factors from the radicand (the number under the square root symbol).The steps to follow includes:
- Identify the perfect square factors: Look for perfect square numbers that evenly divide into the number under the square root. For example, in √72, the perfect square factor is 36 because √36 equals 6.
- Factor out the perfect square: Rewrite the surd using the perfect square factor outside the square root. For example, √72 becomes 6√2.
- If possible, simplify further: Sometimes, you can simplify the expression even more. For instance, if you have √18, you can factor out √9 from it to get 3√2.
- Repeat if necessary: If there are still perfect square factors remaining under the square root, repeat the process until you can no longer simplify.
Example: simplifying surds expressions
Simplify the following:
solution involves breaking down the radicand to the product of it’s prime factor.
(a)
hence we have:
(b) simplifying surds expressions
The idea is to express 12 as products of two numbers. One number results to a rational number after the split. Similarly, 128 can be expressed as a product of 64 and 2 where the square root of 64 results in a rational number.
After expressing all the terms in a simplified for, some of them will have same irrational factor and hence they can be added to make them simpler.
hence we have;
(c) simplifying surds expressions
The idea is to express 128 into two factors such that it is possible to find the 3rd root of one of them and get a whole number. From quick inspection, 128 =64 x 2 and third-root of 64=4.
similarly we can express 250 as a product of 125 and 2. We can be able to deduce that 125 is cube of 5 and hence cube-root of 125 is a rational whole number.
therefore our expression becomes:
Multiplying surds
Surds cab be multiplied the same way we multiply other mathematical constants and variables. The rational factor and the irrational factors are multiplied separately. For example:
Please NOTE: You can only multiply surds that have same irrational factor if only they are in the same order.
The product of two like surds of order 2 is always rational. That is:
From the laws of indices: we recall...
Example 1
Most often, you can simplify unequal surds and they become alike. For example:
Example 2
simplify the expression;
solution
but;
Therefore;
Example: the expression
Simplify the expression below
Solution
we start by expanding the expression:
Note: Always remember to simplify surds first before multiplying
Example

Solution

Example

solution

Related topics
- order of surds
- Introduction to surds
- Simplifying surds
- Multiplying surds
- Rationalizing a denominator
- central tendency in statistics 1: Lazy concise approach
- precisely Integrating trigonometric expressions
- Easy Integration: partial fractions
- Integration by parts-1: Excellent Concise approach
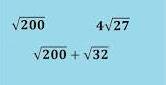

Leave a Reply