focal length by displacement

Focal length by displacement is a method of estimating focal length of a lens by changing position of a lenses and observing the image formed on a screen while distance between object and the lenses is unchanged.

Ensure you have the following apparatus:

Procedure to estimate focal length by displacement

• Estimate the focal length of the lens by focusing a distance object
• Set the apparatus as in figure below ensuring that the distance between the object and the screen is more than 4f where f is the focal length estimated above.

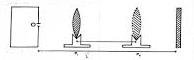
• Obtain the image of the illuminated object on the screen when the lens is at position L₁
• Without changing the position of the object on the screen, move the lens to position L₂ where another clear but diminished image is formed on the screen as shown below.

• measure u and v for position L₁ and the new distance u₁ and v₁ for position L₂.
• Determine the displacement d .

Deriving the displacement formular

from the diagram above, the distance between the point object and the screen is s. from the diagram, it is shown that the distance s is given by u+v.

Advertisement

i. e. s = u+v ………………………………..(1)

The distance between new and original position of the lens will be given by

d=u’- u where u’ is the new object distance and u the original object distance

d can also be obtained from v-v’ which is the original image distance and image distance when the lens is displaced by distance d.

i.e d=u’-u and d = v-v’

but u’=v and v’=u

and therefore:

d=v-u………………………………….(2)

adding (1) and (2);

hence s+ d= u + v + v –u

and so: s + d = 2v and hence;

similarly we can subtract equation 2 from 1 as shown:

hence s- d = u + v –v + u

therefore : s- d = 2u and hence;

from the lens formulae:

we can substitute values of u and v in terms of s and d as obtained in the expressions above. And hence;

the above equation can be simplified into:

finding the lcm of the denominator, we obtain;

and simplifying the above equation in the numerator:

and finding the reciprocal so that we can get f;

from the above equation: s²-d² = 4fs

a plot of s²-d² against s results to a straight line through the origin with a slope equal to 4f.

different values of s are obtained by changing distance between the object and the screen and then calculating the corresponding distance d.

The two positions L₁ and L₂ that represents different positions of the lens are known as the conjugate points.

Related topics

• Focal length by non-parallax method
• Linear Magnification
• Estimating focal length
• focusing a distance object
• The lens formula
• Ray diagrams
• Image formation by thin lenses
• Introduction to thin lenses