When it comes to measuring volumes, we have a variety of units at our disposal. The most commonly units of measuring volumes: include liters (L), milliliters (mL), gallons (gal), and cubic meters (m³). It’s important to understand how to convert between these units to accurately express quantities in different contexts. Whether you’re working with liquids, solids, or gases, mastering volume conversions is essential for precise measurements.
In physics, calculating volume is determining a three-dimensional space occupied by a substance or enclosed in a container using mathematical expressions. It is typically measured in cubic units such as cubic meters (m³) or cubic centimeters (cm³).
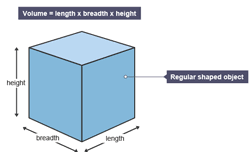
Calculating volume involves using mathematical formulas to determine the volume of regular solids.
Volume as a three dimensional quantity, is obtained when three lengths are multiplied together.
Another popular definition is that volume is a measure of space.
Because volume results from product of three lengths, the SI unit of volume is cubic-meter(m3). That is, SI unit of volume is the cube of the SI unit of length. This tells us that volume is a derived quantity.
However, There are common sub-multiples of volumes like:
- cubic-centimeters (cm3)
- cubic-millimeters (mm3)
- cubic-micrometers (µm3) ………….just to name a few.
1m3 =1m x 1m x1m
but 1m =100cm
hence 1m3 =100cm x 100cm x 100cm = 1000000cm3.
We can as well find units of capacity like litres(l) and millitres(ml).
1 ml =1cm3 .
also 1 litre = 1000ml
1 m3 = 1000 litres.
when you buy a half litre packet of milk from the supermarket, you are actually buying 500ml of milk.
How to convert Units of measuring volumes
we will have some examples of how to convert units of measuring volumes from one unit to another.
if we are converting a large unit into a smaller unit, we will need to multiply the larger unit with the multiplying factor.
If we are converting a smaller unit into a larger unit, we may need to divide the smaller unit a conversion factor. see the illustration below.
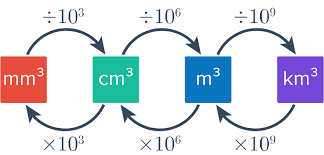
Example on converting units of measuring volume
Express 43.5mm3 into m3.
Solution
1 cm = 10mm
1cm3 = 10mm x 10mmx10mm = 1000mm3
therefore: 1cm3 is equivalent to 1000mm3 .
if 1cm3 = 1000mm3 .
let x cm3 = 43.55mm3
we cross multiply the two expressions so that we obtain:
x cm3 x 1000mm3 = 1cm3 x 43.55 mm3
we now need to then convert the value above into cubic mete which is the requirement of our problem
1m3 = 1m x 1m x 1m
but 1m= 100cm
Therefore 1m3 = 100cm x 100cm x 100cm: therefore;
1m3 = 1000000cm3
let x m3 = 0.0436 cm3
This shows that: 43.5mm3 = 0.00000000435 m3
Example on converting units of measuring volume
convert 0.00006 m3 into cm3
Solution
as illustrated in the example above:
1m3 = 1000000cm3
let 0.00006 m3 = x
hence:
practice Questions
(a) The radius of a typical atom is considered to have a volume of 10-10m3. Express the given volume in:
- mm3
- cm3
- µm3
(b) A liquid is measured as 18.5 litres. Express this capacity in:
(I) cubic centimeters
(ii) cubic meters
conclusion
Measuring volume may involves calculating the volume of an object or substance. To convert between different units of volume, we can use conversion factors. For example, if 1 cm³ = 1000 mm³, then the conversion factor between cm³ and mm³ is 1000. Similarly, to convert cm³ to m³, we can use the fact that 1 m³ = 1000000 cm³. By applying these conversion factors, we can accurately convert volume measurements from one unit to another.

Leave a Reply to Conical pendulum – precisestudy Cancel reply